第4回 スコープ、オブジェクト指向と読みやすいコード

目次

• 第4回 スコープ、オブジェクト指向と読みやすいコード
• 目次
• 前回の復習
  • 複雑な制御構文
    • Case文
    • While文
      • each文
      • breakとnext
  • 修飾子
  • 再帰関数
• スコープ
  • グローバル変数
• オブジェクト指向
• 読みやすいコード
  • 変数・関数名
  • 関数
  • コメントアウト
• 演習
  • 演習問題4a
  • 演習問題4b
  • 演習問題4c
  • 以下上級者向け問題
  • 演習問題4d
  • 演習問題4e
  • 演習問題4f(ジャッジはなし)

前回の復習

前回は再帰関数など少し難しい内容が多く説明が足りなかった部分もあるかもしれません。

本当の詳しいところは、今後授業や競プロなどで興味があれば是非沼にハマっていってください。

この講習の目的としては、制御構文や関数を扱えるという部分なので前回の後半の内容をすべて理解していなくても大丈夫です。

複雑な制御構文

Case文

def getClass(age)
  if 0..2
    "幼児"
  when 3..6
    "小児"
  when 7..12
    "子供"
  when 13..18
    "若者"
  else
    "大人"
  end
end

case AとしたときAとwhenで指定された部分が一致する処理を行いってくれます。elseはどの条件にも当てはまらないときに呼ばれる。

1つの値に対して複数の条件分岐をする場合に完結に書くことができる。

While文

while文は条件を満たす間は処理を行う処理。

def countdown(n)
  while n > 0 do
    puts n
    n = n -1
  end
end

のような処理をすると、n > 0を満たす間はn = n - 1をするので、nから順にカウントダウンされていきます。

each文

data = [1, 2, 3]
sumA = 0.0
sumB = 0.0
for num in data do
  sumA += num
end
data.each do |num|
  sumB += num
end

のように配列から順番に要素を取り出して処理をすることが可能です。

breakとnext

breakはループを強制的に抜ける命令で

10.times do |i|
  break if i > 5
  puts i
end

このように、iが5より大きくなるとbreakが呼び出されてfor文から強制的に抜けるので、

0
1
2
3
4
5

となります。

また、next文を使うと特定の条件で処理をスキップすることもでき、

10.times do |i|
  next if i % 2 == 0
  puts i
end

のようにすると、iが2の倍数のときにnextが呼び出されて処理がスキップされます。 つまりは、

1
3
5
7
9

のように奇数だけが出力されるようになります。

修飾子

ifやwhileなどの文は

def fac(n)
  return 1 if n == 0
  return n * fac(n-1)
end

のように、処理 if 条件などのようにすると1行で書くことが可能。

再帰関数

def fac(n)
  return 1 if n == 0
  return n * fac(n-1)
end

のようなコードが有る場合に、例えば、n=3を入れた時の動作を見てみると

fac(3) => 3 * fac(2)
fac(2) => 2 * fac(1)
fac(1) => 1

順番に代入してみると、

fac(3) => 3 * 2 * 1 = 6

となります。

このように関数の中で関数を呼び出すことが可能。

• 再帰関数を使うと漸化式などをそもまま実装できる

• 繰り返しで書くよりも完結に書ける場合もある

ただし、関数を呼び出す回数が多くなりすぎるとエラーが起きるので注意。

再帰関数を使いこなせると色々なアルゴリズムを実装できるが、少し複雑になるのでこの講習では省略。

キーワード

• 動的計画法(メモ化再帰)
• 幅優先探索
• 関数型プログラミング

沼にハマりたい人は是非

スコープ

今回の講習では基本的に関数ベースで話しをしていたため、あまり登場していなかったが補足。

Rubyで今まで扱ってきた変数にはいくつか種類があった。

• ローカル変数 (今までこれを使ってた)
• インスタンス変数
• クラス変数
• グローバル変数

name = "Void"

def greet(name)
  script =  "Hello!" + name + "!"
  puts(script)
end

greet("Void")
puts(script)

これを実行すると、

Hello!Void!
Error: eval:9:in `<main>': undefined local variable or method `script' for main:Object (NameError)

のようにエラーが発生する。

関数の中で定義された変数は関数のみで有効。

スコープは、変数の有効範囲のこと。

グローバル変数

では、関数の中で定義した変数を外でも使いたい場合は？

name = "Void"

def greet(name)
  $script =  "Hello!" + name + "!"
  puts($script)
end

greet("Void")
puts($script)

これだと、

Hello!Void!
Hello!Void!

のように正しく表示される。

変数の先頭に、$をつけて$scriptあげるとグローバル変数と呼ばれるものになる。

グローバル変数のスコープ(有効範囲)はプログラム全体なので、どこからでも参照できる。

オブジェクト指向

プログラミング言語にはいくつか種類がある。

• 手続き型言語(C言語やBASICなど)
• オブジェクト指向言語(RubyやPythonなど)
• 関数型言語(GoやHaskellなど)

この中でも、Rubyはオブジェクト指向という考え方に基づいた言語になっている。

オブジェクト指向の重要な3つの概念は、

• カプセル化(隠蔽)
• 継承
• ポリモーフィズム

今回は雰囲気だけ。

プログラムでは、クラスと呼ばれる関数やデータをまとめたものを扱います。

例えば、ラインをトレースするロボットを制御することを考えてみます。

このロボットをパーツごとに分解してみると、大きく分けると

• コントローラー
• センサー
• バッテリー
• モーター

に分けられます。

• カプセル化

普通にモーターを制御する場合には、

モータードライバの仕様を理解した上で、それを駆動させるための信号を作成するプログラムを作らなくてはいけませんが、制御する側はそんなハードウェアのことなんて気にしたくないですよね。

つまりは、モーターをどっちに回すのかと速度を指定すれば勝手にモーターが回ってくれれば良いですよね。

あと、モータードライバを変更するたびに変更するの面倒ですよね。一回、作ったら他のロボットでも使いまわしたい。

このように、内部の処理をブラックボックス化してあげることをカプセル化といいいます。

• 継承

では、車を動かすためにモーターを制御するクラスを作りました。

車の「直進」「止まる」「曲がる」といったいったようなものを実装するときに、それぞれでまたモーターを制御する設定を書くのは面倒ですよね。

そこで、基本的な設計図を用意して他の必要な部分はそれぞれカスタマイズします。これが継承です。

では、実際にRubyでどのように実装されるのか見てみます。

class ClassName
def method_name(arg1,arg2,...)
  処理
end

instance = ClassName.new()
instanace.medhot_name()

RubyではこのようにClassを定義します。

クラスを実行する際には、インスタンスと呼ばれる実体を生成します。

class Motor
  def stop()
    puts "Stop"
  end
  def move(speed)
    puts "MOVE #{speed}"
  end
end

rightMotor = Motor.new
rightMotor.move(1.0)
rightMotor.stop()

実行すると、

MOVE 1.0
Stop

サーボモータ(角度をしてできるモーター)を追加してみる。

class Motor
  def stop()
    puts "Stop"
  end
  def move(speed)
    puts "MOVE #{speed}"
  end
end

class Servo < Motor
  def moveDegree(degree)
    puts "MOVEDEG #{degree}"
  end
end

rightMotor = Servo.new
rightMotor.moveDegree(30)
rightMotor.stop()

これを実行すると、

MOVEDEG 30
Stop

のように、Motorクラスに対して機能を追加しているような感じ。

オブジェクト指向は、実際にコードを試行錯誤してみると良い設計や機能をつかめるはず。

読みやすいコード

1人でコードを書いているだけならいいが、チーム開発などでは他の人が読めるコードを書くことが必要になる。特に、ぐちゃぐちゃなコードを書いてしまうと、のちのちの自分もわけがわからなくなってしまう。

変数・関数名

変数名を定義するときに適当な名前をつけていませんか?

例えば、次のようなうるう年か判定する関数があったとします。 ここでは仮に2022~2027までの5年間を判定します。

def uruudoshi(toshi)
  if toshi == 2022 then
    return false
  elsif toshi == 2023 then
    return false
  elsif toshi == 2024 then
    return true
  elsif toshi == 2025 then
    return false
  elsif toshi == 2026 then
    return false
  elsif toshi == 2027 then
    return false
  end
end

折角なのでもうすこし和風にしてみましょう。

def うるう年かどうか(年)
  if 年 == 2022 then
    return false
  elsif 年 == 2023 then
    return false
  elsif 年 == 2024 then
    return true
  elsif 年 == 2025 then
    return false
  elsif 年 == 2026 then
    return false
  elsif 年 == 2027 then
    return false
  end
end

変数名や関数名をつける時のポイント

• その名前を見ただけで、何を表す変数、関数なのかすぐに理解できるようにする
• 基本的に英語でつける このサイトとか便利
• 汎用的な言葉を避けて分かりやすく

既存のライブラリなどを参考にすると良いかも。

あとは、命名規則を統一すると良いです。

• camelCase (単語の先頭を大文字)
• snake_case (単語の間をアンダーバー)
• kebab-case (単語の間をハイフン)

例えば、今回の場合だと

# Rubyの場合true/falseを返す関数は?、破壊的な関数は!をつける慣習
def isLeapYear?
  if n % 4 != 0
    puts false
  elsif n % 100 == 0 && n % 400 !=0
    puts true
  else
    puts true
  end
end

のように実装できます。

うるう年問題はあるますが、2027までなら大丈夫。

関数

関数はなるべく機能ごとに簡単に実装します。

もし、長くなりそうな場合や使い回すことができそうな場合は関数にします。

コメントアウト

コードを書くときに適切にコメントアウトを残しておくと、他の人が読んだときや自分が読んだときに役に立ちます。

コードを読んでみると面白い。

# これは魔法。触っちゃダメ。
# 誰もコメントを読んでくれない！
# THANK YOU MARIO! BUT OUR PRINCESS IS IN ANOTHER CASTLE!
# TODO: もう全部消す
# これ書いた奴バカじゃねーの…全然動かねーよ！

なんでもかんでもコメントするよりは、考えたロジックなどパット見ではわからないことを書く。場合にもよるが。

def getPrimeList(max)
  list = (2..max).to_a #2からmaxまでの配列(なくても良いかも)
  prime_list = []
  sqrt = Math.sqrt(max).floor
  # 倍数を消す(エラトステネスの篩)
  while val = list.shift
    prime_list << val
    if val > sqrt
      break
    end
    list.delete_if{|num| num % val == 0}
  end
  return prime_list.concat(list)
end

演習

今回の扱った内容は少し難しいため演習問題は基本的にこれまでの内容の応用です

演習問題4a

2Dゲーム開発者のあなたは円と任意の壁との当たり判定を実装したいと思っています。

ここで壁は直線であり\(ax+by+c=0\)で与えられます。また、円の中心座標\((x_0, y_0)\)であり半径は\(r\)で与えられます。

このとき、円と壁が接触しているか判定する関数isTouched(a,b,c,x0,y0,r)を作成せよ。

ただし、壁抜けを防止するために接触の判定には1.0の幅をもたせる。

制約
すべての値は整数として与えられる

\[\begin{align} 直線:& ax+by+c=0\\ 円:& (x-x_0)^2+(y-y_0)^2=r^2 \end{align}\]

のグラフをGeoGebraなどで描画して試すと良いかも

入出力例

isTouched(49,27,40,55,59,77) => true

演習問題4b

これまでやってきた内容は基本的な文法などです。プログラミングで重要なのは、アルゴリズムを考えそれを実装する力でもあったりします。 アルゴリズムの勉強としてよくあるのが数を並べ替えるソートです。 整数が配列として与えられたときに、それらを小さい順に並べ替えて出力する関数sort(data)を作成する。

制約
データはすべて整数
配列の要素数Nは5以上20以下

入出力例

sort([1, 3, 4, 5, 2]) => [1, 2, 3, 4, 5]

ヒント

色々なアルゴリズムがあるが、バブルソートと呼ばれるアルゴリズムを紹介する。

• 隣接する要素と比較し順序が逆であれば入れ替える
• すべてがソートされるまで繰り返す

配列dataでi番目とi+1番目の要素を入れ替える場合は,

data[i], data[i+1] = data[i+1], data[i]

のように書けます。

演習問題4c

AさんとBさんがじゃんけんをした結果が配列として与えられる。

このとき、AさんとBさんの勝敗を出力する関数judge(arrA, arrB)を作成する。

出力は、Aさんが買った場合には"A"、Bさんが買った場合には"A"、引き分けの場合は"DRAW"を出力する。

なお、じゃんけんの結果は0がグー、1がチョキ、2がパーとして与えられる。

制約
じゃんけんの回数は1以上20以下である。

入出力例

judge([1,1,0],[2,2,2]) => "A"

ヒント じゃんけんの関係に注目すると賢く判定できます

以下上級者向け問題

演習問題4d

コンピューターを用いて数値シミュレーションをすることはコンピューターの活用としてよくあります。

では、コンピューターを用いて定積分を解いてみましょう。

\[\int_a^b f(x) dx\]

が与えられたときにその近似解を求める関数を作成せよ。

ただし、関数f(x)は文字列"x**2+x"のように与えられ

x = 1.0
eval(f) => 2.0

として、eval関数を用いてf(x)の結果を取得できる。

ヒント

定積分をシュミレートする方法には、色々ありますがここではシンプルな台形公式を用いた方法を紹介します。

積分区間を分割してあげて、足し合わせることによって求める方法を数値積分といいます。

ここで、積分区間を\(n\)個に分割してあげて、その微小な幅を\(h=(b-a)/n\)とします。

このとき、図のように少区間ごとに台形で分割してあげます。

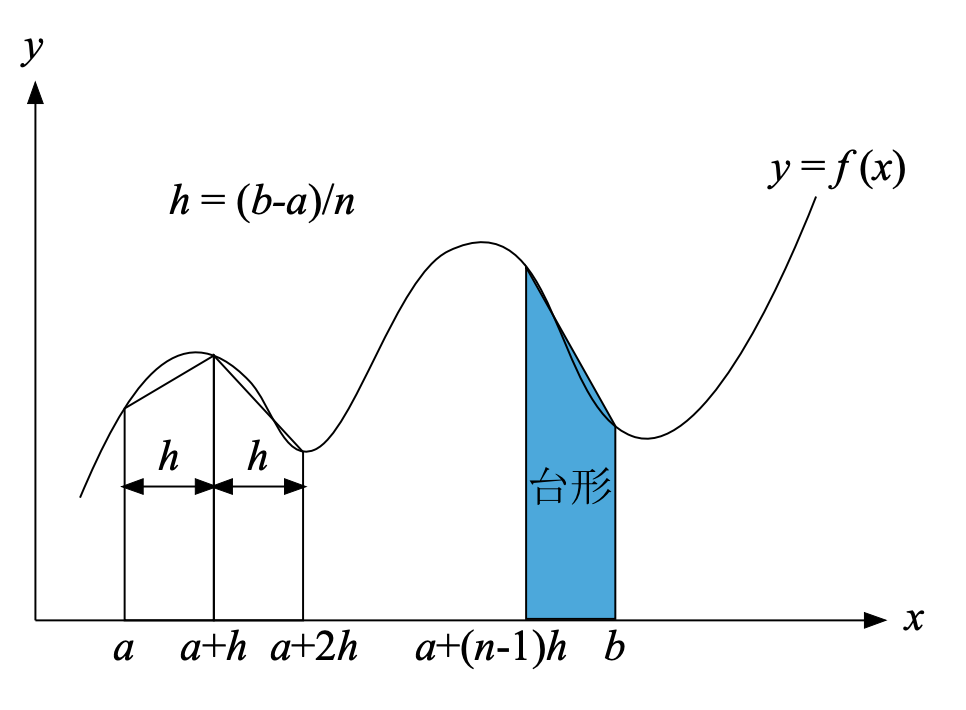
すると、1つの台形の面積\(\Delta A(x_i)\)は、

\[\Delta A(x_i) = \frac{h}{2} \{ f(a+i\cdot h)+f(a+(i+1)\cdot h) \}\]

として表されます。

これを利用すると、

\[\begin{align*} \int_a^b f(x) dx &\simeq \sum_{i=1}^n \Delta A(x_i)\\ &= \sum_{i=1}^n \frac{h}{2} \{ f(a+i\cdot h)+f(a+(i+1)\cdot h) \} \end{align*}\]

として近似できます。

制約
a,bは実数
f(x)は区間内においてすべて正
小数点以下2桁までの精度で判定

getArea(0,1,"Math.sqrt(x**2+1)") => 1.14

演習問題4e

4aの問題はいろいろなアルゴリズムがあります。

その中でも、1で示したバブルソートは少し遅いアルゴリズムですので、そのアルゴリズムを高速化して大量のデータを合計500ms以下でソートできるように改良してください。

キーワード

• クイックソート
• ヒープソート
• ボゴソート
• バイナリソート

制約
データはすべて整数
配列の要素数Nは1000以上200以下

演習問題4f(ジャッジはなし)

Rubyの型はすべてClassにより実装されています。そのため、新しく型を追加したり上書きすることが可能です。

例えば、Classを使うと

class String
  def だ！
    self
  end
end

class C名前 < String
  def initialize(名前)
    self.replace 名前
  end

  def self.命名(名前)
    self.new 名前
  end

  def は(値)
    self.replace 値
  end

  def の名前
    return self
  end

  def 逆にする
    return self.reverse
  end

  def の名前を教えて
    puts self
  end
end

のようにすると、

私 = C名前.命名("平地")
私.の名前を教えて
私.は 私.の名前.逆にする
私.の名前を教えて
私.は "山田".だ！
私.の名前を教えて

のように日本語っぽい謎のプログラムを書くこともできます。

ここで、実際に新しい型を定義して複素数の演算をするClassを作成せよ。

テンプレートとして以下を示す。

class Comp
  def initialize(a, b)
    # 複素数 a+bi
    @a = a; @b = b
  end

  def getReal
    @a
  end

  def getImagine
    @b
  end

  def to_s
    str = ""
    if @a != 0 then str += "#{@a}" end
    if @a != 0 && @b > 0 then str += "+" end
    if @b != 0 then str += "#{@b}i" end
    str
  end

  def abs
    # 複素数の大きさを返す
    # ここに実装
  end

  def conj
    # 共役複素数を返す
    # ここに実装
  end

  def +(x)
    # 複素数の和を返す
    # ここに実装
  end

  def -(x)
    # 複素数の差を返す
    # ここに実装
  end

  def *(x)
    # 複素数の席を返す
    # ここに実装
  end

  def **(n)
    # 複素数の累乗を返す
    # ここに実装
  end

  def /(x)
    # 複素数の割り算を返す
    if x.getImagine != 0
      # 分母に虚数があるなら実数化する
      # ここに実装
    end
    # ここに実装
  end
end

正しく実装できると、

a = Comp.new(0, 1) # i
b = Comp.new(1, 1) # 1+i
puts a + b => 1 + 2i
puts a - b => -1
puts a * b => -1 + 1i
puts a / b => 0.5 + 0.5i

のようにして正しく計算をすることができる。

なお、@aなどの変数はクラスの中で使用するクラス変数です。